基于物理的渲染（Physically Based Rendering , PBR）技术，自迪士尼在SIGGRAPH 2012上提出了著名的“迪士尼原则的BRDF（Disney Principled BRDF）”之后，由于其高度的易用性以及方便的工作流，已经被电影和游戏业界广泛使用。

公式总结

迪士尼原则的BRDF

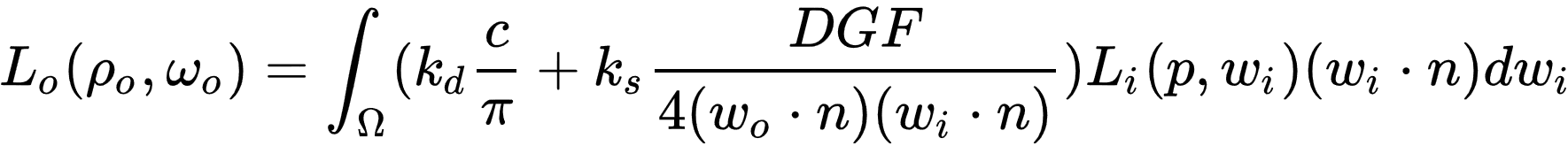
以上公式是用数学语言描述，翻译成中文就是

以下是对PBR基础理念的概括：

微平面理论（Microfacet Theory）。微平面理论是将物体表面建模成做无数微观尺度上有随机朝向的理想镜面反射的小平面（microfacet）的理论。在实际的PBR 工作流中，这种物体表面的不规则性用粗糙度贴图或者高光度贴图来表示。
能量守恒（Energy Conservation）。出射光线的能量永远不能超过入射光线的能量。随着粗糙度的上升镜面反射区域的面积会增加，作为平衡，镜面反射区域的平均亮度则会下降。
菲涅尔反射（Fresnel Reflectance）。光线以不同角度入射会有不同的反射率。相同的入射角度，不同的物质也会有不同的反射率。万物皆有菲涅尔反射。F0是即 0 度角入射的菲涅尔反射值。大多数非金属的F0范围是0.02~0.04，大多数金属的F0范围是0.7~1.0。
线性空间（Linear Space）。光照计算必须在线性空间完成，shader 中输入的gamma空间的贴图比如漫反射贴图需要被转成线性空间，在具体操作时需要根据不同引擎和渲染器的不同做不同的操作。而描述物体表面属性的贴图如粗糙度，高光贴图，金属贴图等必须保证是线性空间。
色调映射（Tone Mapping）。也称色调复制（tone reproduction），是将宽范围的照明级别拟合到屏幕有限色域内的过程。因为基于HDR渲染出来的亮度值会超过显示器能够显示最大亮度，所以需要使用色调映射，将光照结果从HDR转换为显示器能够正常显示的LDR。
物质的光学特性（Substance Optical Properties）。现实世界中有不同类型的物质可分为三大类：绝缘体（Insulators），半导体（semi-conductors）和导体（conductors）。在渲染和游戏领域，我们一般只对其中的两个感兴趣：导体（金属）和绝缘体（电解质，非金属）。其中非金属具有单色/灰色镜面反射颜色。而金属具有彩色的镜面反射颜色。即非金属的F0是一个float。而金属的F0是一个float3，如下图。

1.镜面反射BRDF模型（Specular BRDF）

游戏业界目前最主流的基于物理的镜面反射BRDF模型是基于微平面理论（microfacet theory）的Microfacet Cook-Torrance BRDF。

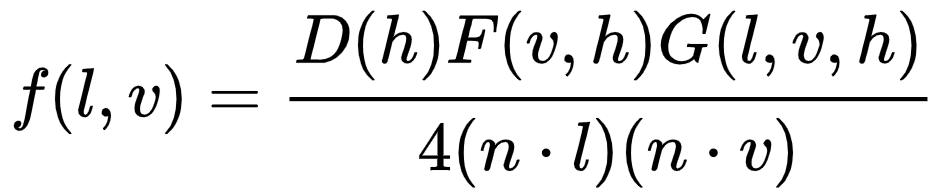
D(h) : 法线分布函数（Normal Distribution Function），描述微面元法线分布的概率，即正确朝向的法线的浓度。即具有正确朝向，能够将来自l的光反射到v的表面点的相对于表面面积的浓度。
F(l,h) : 菲涅尔方程（Fresnel Equation），描述不同的表面角下表面所反射的光线所占的比率。
G(l,v,h) : 几何函数（Geometry Function），描述微平面自成阴影的属性，即m = h的未被遮蔽的表面点的百分比。
分母 4(n·l)(n·v）：校正因子（correctionfactor），作为微观几何的局部空间和整个宏观表面的局部空间之间变换的微平面量的校正。

关于Cook-Torrance BRDF，需要强调的两点注意事项：

对于分母中的点积，仅仅避免负值是不够的 ,也必须避免零值。通常通过在常规的clamp或绝对值操作之后添加非常小的正值来完成。
Microfacet Cook-Torrance BRDF是实践中使用最广泛的模型，实际上也是人们可以想到的最简单的微平面模型。它仅对几何光学系统中的单层微表面上的单个散射进行建模，没有考虑多次散射，分层材质，以及衍射。Microfacet模型，实际上还有很长的路要走。

1.D项法线分布函数（Normal Distribution Function, NDF）

业界较为主流的法线分布函数是GGX（Trowbridge-Reitz），因为具有更好的高光长尾：

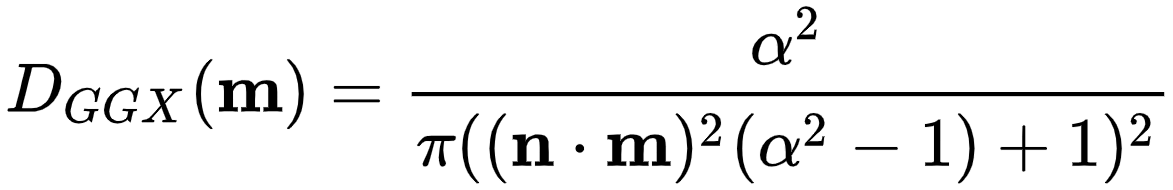
2.F项菲涅尔系数（Fresnel）

业界方案一般都采用Schlick的Fresnel近似，因为计算成本低廉，而且精度足够：

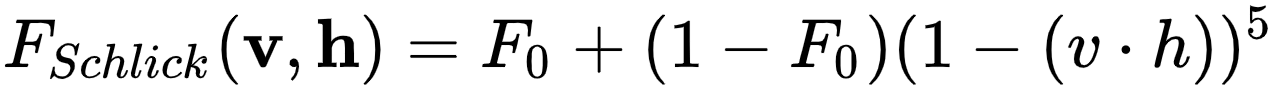
3.G项几何阴影遮蔽函数(Geometry Shadow function)

几何函数也使用粗糙度作为输入参数，更粗糙意味着微平面产生自阴影的概率更高。几何函数使用由GGX和Schlick-Beckmann组合而成的模拟函数Schlick-GGX：

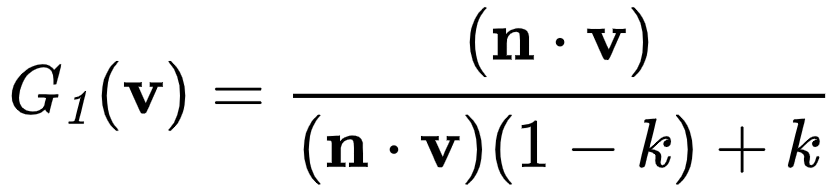
这里的k是使用粗糙度α计算而来的，用于直接光照和IBL光照的几何函数的参数：

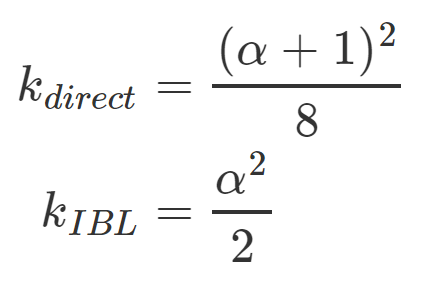
为了有效地模拟几何体，我们需要同时考虑两个视角，视线方向（几何遮挡）跟光线方向（几何阴影），我们可以用Smith函数将两部分放到一起：

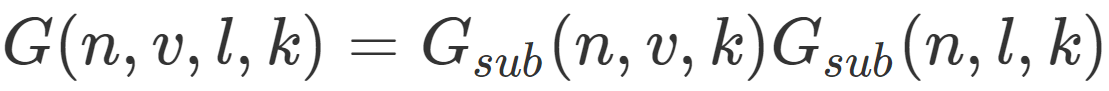
2.基于物理的环境光照（Physically Based Environment Lighting ）

漫反射环境光照部分一般采用传统IBL中辉度环境映射（Irradiance Environment Mapping）技术，并不是基于物理的特有方案，这里暂不讨论。

而基于物理的镜面反射（Specular）环境光照，业界中一般会采用基于图像的光照（IBL）的方案。要将基于物理的BRDF模型与基于图像的光照（IBL）一起使用，需要求解光亮度积分（Radiance Integral），而求解光亮度积分通常会使用重要性采样（Importance Sample）。

1.预过滤环境贴图（Pre-filtered environment map）

第一项可以理解为对光亮度求均值。经过n= v= r的假设，仅取决于表面粗糙度（surface roughness）和反射矢量（reflection vector）。这一项，业界的做法比较统一（包括UE4和COD：Black Ops 2等），采用的方案主要借助预过滤环境贴图，用多级模糊的mipmap来存储模糊的环境高光:

也就是说，第一项直接使用cubemap 的mip级别采样输入即可。

2.环境BRDF （Environment BRDF）

第二项即镜面反射项的半球方向反射率（hemispherical-directional reflectance），可以理解为环境BRDF（Environment BRDF）。其取决于仰角θ，粗糙度α和菲涅耳项F。通常使用Schlick近似来近似F，其仅在单个值F0上参数化，从而使Rspec成为三个参数（仰角θ（NdotV），粗糙度α、F0）的函数。

这一项的主要流派有两个，UE4的2D LUT，以及COD：OP2的解析拟合。

1.流派1：2D LUT

UE4在[Real Shading in Unreal Engine 4, 2013]中提出，第二个求和项，使用Schlick近似后， F0可以从积分中分出来：

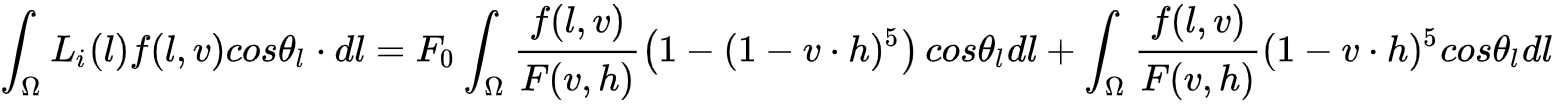
上式留下了两个输入（Roughness 和 cos θv）和两个输出（缩放和向F0的偏差（a scale and bias to F0）），即把上述方程看成是F0 * Scale + Offset的形式。我们预先计算此函数的结果并将其存储在2D查找纹理（LUT，look-up texture）中。

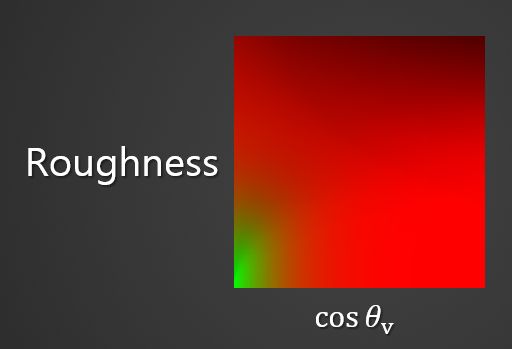
这张红绿色的贴图，输入roughness、cosθ，输出环境BRDF镜面反射的强度。是关于roughness、cosθ与环境BRDF镜面反射强度的固有映射关系。可以离线预计算。

具体的取出方式为：

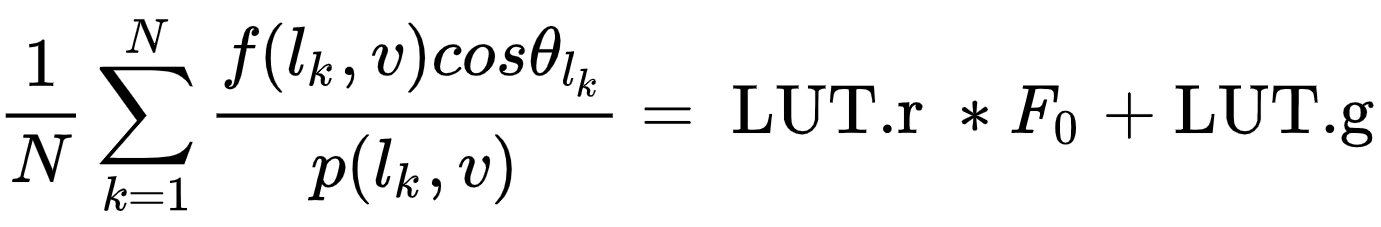
即UE4是通过把Fresnel公式的F0提出来，组成F0 * Scale +Offset的方式，再将Scale和Offset的索引存到一张2D LUT上。靠roughness和 NdotV进行查找。

2.流派2：解析拟合

COD：Black Ops 2的做法，是通过数学工具Mathematica中的数值积分拟合出曲线，即将UE4离线计算的这张2D LUT用如下函数进行了拟合：

float3 EnvironmentBRDF( float g, float NoV, float3 rf0 )
{
    float4 t = float4( 1/0.96, 0.475, (0.0275 - 0.25 \* 0.04)/0.96, 0.25 );
    t *= float4( g, g, g, g );
    t += float4( 0, 0, (0.015 - 0.75 * 0.04)/0.96, 0.75 );
    float a0 = t.x * min( t.y, exp2( -9.28 * NoV ) ) + t.z; float a1 = t.w;
    return saturate( a0 + rf0 * ( a1 - a0 ) );
}

需要注意的是，上面的方程是基于Blinn-Phong分布的结果，https://knarkowicz.wordpress.com/2014/12/27/analytical-dfg-term-for-ibl/一文中提出了基于GGX分布的EnvironmentBRDF解析版本：

float3 EnvDFGLazarov( float3 specularColor, float gloss, float ndotv )
{
    float4 p0 = float4( 0.5745, 1.548, -0.02397, 1.301 );
    float4 p1 = float4( 0.5753, -0.2511, -0.02066, 0.4755 );
    float4 t = gloss * p0 + p1;
    float bias = saturate( t.x * min( t.y, exp2( -7.672 * ndotv ) ) + t.z );
    float delta = saturate( t.w );
    float scale = delta - bias;
    bias *= saturate( 50.0 * specularColor.y );
    return specularColor * scale + bias;
}

上式中的specularColor即F0。

EnvironmentBRDF函数的输入参数分别为光泽度gloss，NdotV，F0。和UE4的做法有异曲同工之妙，但COD：Black Ops 2的做法不需要额外的贴图采样，这在进行移动端优化时，是不错的选择。

虽然我们目前主要关注的是实时渲染（实时光栅图形学相关，暂时不关注实时光线追踪）领域，但很多时候，实时渲染也需要涉及到预计算，尤其是IBL相关的预计算，所以或多或少会用到离线渲染相关的知识。

以下是与实时渲染结合相对紧密的离线渲染相关的核心主题以及概括总结（主要是统计学与概率相关）：

重要性采样（ Importance Sample）：蒙特卡洛积分的一种采样策略。思路是基于分布函数，尽量对被积函数分布可能性较高的区域进行采样。
多重要性采样（Muti Importance Sampling, MIS） ：估算某一积分时，基于多个分布函数获取采样，并期望至少某一分布与被积函数形状适配。即根据各种技术对采样进行加权计算，进而消除源自被积函数值与采样密度不匹配造成的较大反差。
大数定律（Law of Large Numbers） ：在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。即偶然中包含着某种必然。
蒙特卡洛方法（Monte Carlo Methods） ：一种以概率统计理论为指导的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。
低偏差序列（Low-discrepancy sequence） ：一种确定生成的超均匀分布列，也称为拟随机列、次随机列，常见低偏差序列有Hammersley，Halton等。
拟蒙特卡罗方法（Quasi-Monte Carlo Method） ：使用低差异列来进行数值积分和研究其它一些数值问题的方法。等

Physically Based Rendering

基于物理的渲染

公式总结

1.镜面反射BRDF模型（Specular BRDF）